El código de este blog, junto con el conjunto de datos, está disponible en el siguiente enlace https: // github.com / shekharpandey89 / k-means
La agrupación en clústeres de K-Means es un algoritmo de aprendizaje automático no supervisado. Si comparamos el algoritmo de agrupamiento no supervisado de K-Means con el algoritmo supervisado, no es necesario entrenar el modelo con los datos etiquetados. El algoritmo K-Means se utiliza para clasificar o agrupar diferentes objetos según sus atributos o características en un número K de grupos. Aquí, K es un número entero. El K-Means calcula la distancia (usando la fórmula de la distancia) y luego encuentra la distancia mínima entre los puntos de datos y el grupo de centroides para clasificar los datos.
Entendamos las K-medias usando el pequeño ejemplo usando los 4 objetos, y cada objeto tiene 2 atributos.
| ObjectsName | Atributo_X | Atributo_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-medias para resolver el ejemplo numérico:
Para resolver el problema numérico anterior mediante K-Means, tenemos que seguir los siguientes pasos:
El algoritmo K-Means es muy simple. Primero, tenemos que elegir cualquier número aleatorio de K y luego elegir los centroides o el centro de los grupos. Para elegir los centroides, podemos elegir cualquier número aleatorio de objetos para la inicialización (depende del valor de K).
Los pasos básicos del algoritmo K-Means son los siguientes:
- Continúa funcionando hasta que ningún objeto se mueva de sus centroides (estable).
- Primero elegimos algunos centroides al azar.
- Luego, determinamos la distancia entre cada objeto y los centroides.
- Agrupar los objetos según la distancia mínima.
Entonces, cada objeto tiene dos puntos como X e Y, y se representan en el espacio del gráfico de la siguiente manera:
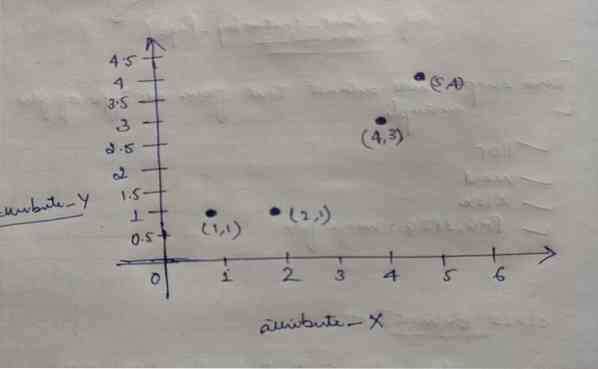
Entonces, inicialmente elegimos el valor de K = 2 como aleatorio para resolver nuestro problema anterior.
Paso 1: Inicialmente, elegimos los dos primeros objetos (1, 1) y (2, 1) como nuestros centroides. El siguiente gráfico muestra lo mismo. A estos centroides los llamamos C1 (1, 1) y C2 (2,1). Aquí, podemos decir que C1 es group_1 y C2 es group_2.
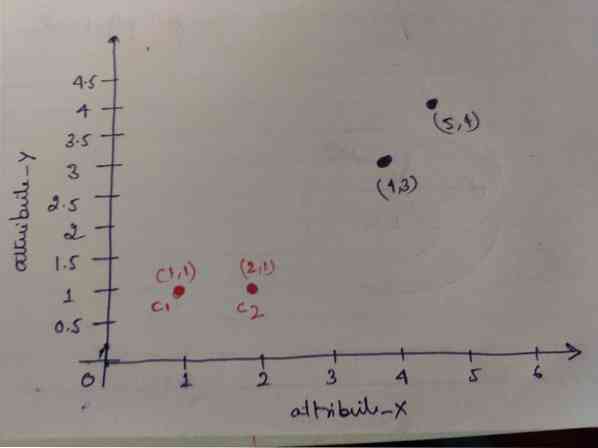
Paso 2: Ahora, calcularemos cada punto de datos de objeto a centroides usando la fórmula de distancia euclidiana.
Para calcular la distancia usamos la siguiente fórmula.

Calculamos la distancia de los objetos a los centroides, como se muestra en la imagen de abajo.

Entonces, calculamos la distancia del punto de datos de cada objeto a través del método de distancia anterior, finalmente obtuvimos la matriz de distancia como se indica a continuación:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grupo 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | Grupo 2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Ahora, calculamos el valor de distancia de cada objeto para cada centroide. Por ejemplo, los puntos del objeto (1,1) tienen un valor de distancia a c1 es 0 y c2 es 1.
Como, de la matriz de distancias anterior, encontramos que el objeto (1, 1) tiene una distancia al cluster1 (c1) es 0 y al cluster2 (c2) es 1. Entonces el objeto uno está cerca del clúster1 en sí.
De manera similar, si verificamos el objeto (4, 3), la distancia al cluster1 es 3.61 y al cluster2 es 2.83. Entonces, el objeto (4, 3) cambiará a cluster2.
De manera similar, si busca el objeto (2, 1), la distancia al cluster1 es 1 y al cluster2 es 0. Entonces, este objeto cambiará a cluster2.
Ahora, de acuerdo con su valor de distancia, agrupamos los puntos (agrupación de objetos).
G_0 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | grupo 1 |
| 0 | 1 | 1 | 1 | Grupo 2 |
Ahora, de acuerdo con su valor de distancia, agrupamos los puntos (agrupación de objetos).
Y finalmente, el gráfico se verá a continuación después de hacer la agrupación (G_0).
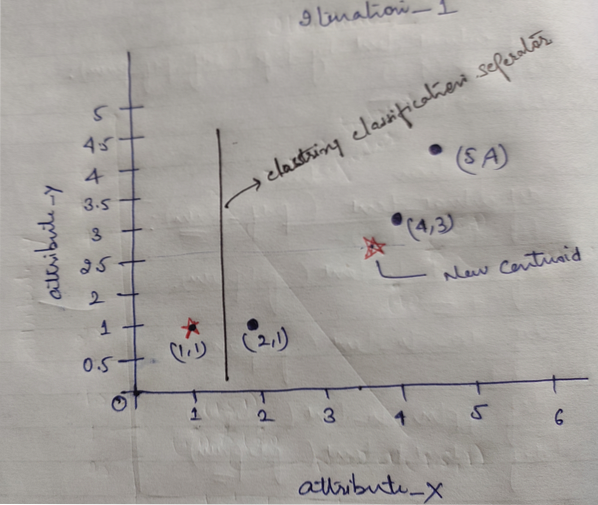
Iteración_1: Ahora, calcularemos nuevos centroides a medida que los grupos iniciales cambiaron debido a la fórmula de distancia como se muestra en G_0. Entonces, el grupo_1 tiene solo un objeto, por lo que su valor sigue siendo c1 (1,1), pero el grupo_2 tiene 3 objetos, por lo que su nuevo valor de centroide es 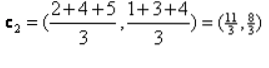
Entonces, nuevos c1 (1,1) y c2 (3.66, 2.66)
Ahora, nuevamente tenemos que calcular toda la distancia a los nuevos centroides como calculamos antes.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grupo 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | Grupo 2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (agrupación de objetos): Ahora, en nombre del cálculo de la nueva matriz de distancia (DM_1), lo agrupamos de acuerdo con eso. Entonces, cambiamos el objeto M2 de group_2 a group_1 como la regla de distancia mínima a los centroides, y el resto del objeto será el mismo. Entonces, la nueva agrupación será la siguiente.
G_1 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupo 1 |
| 0 | 0 | 1 | 1 | Grupo 2 |
Ahora, tenemos que calcular los nuevos centroides nuevamente, ya que ambos objetos tienen dos valores.
Entonces, los nuevos centroides serán 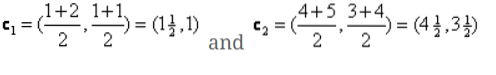
Entonces, después de obtener los nuevos centroides, la agrupación se verá a continuación:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
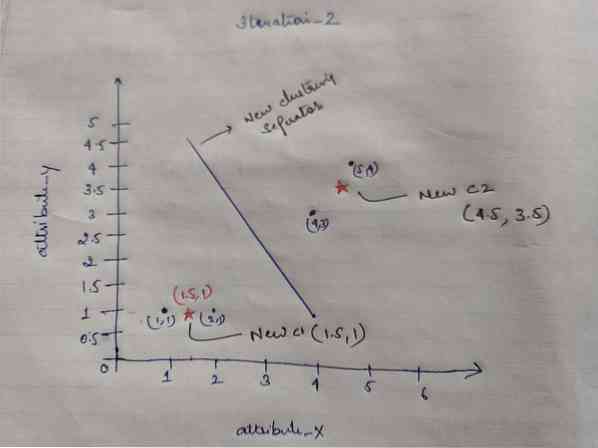
Iteración_2: Repetimos el paso donde calculamos la nueva distancia de cada objeto a los nuevos centroides calculados. Entonces, después del cálculo, obtendremos la siguiente matriz de distancia para iteration_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | grupo 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | Grupo 2 |
A B C D
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Nuevamente, hacemos las asignaciones de agrupamiento en base a la distancia mínima como lo hicimos antes. Entonces, después de hacer eso, obtuvimos la matriz de agrupamiento que es la misma que G_1.
G_2 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupo 1 |
| 0 | 0 | 1 | 1 | Grupo 2 |
Como aquí, G_2 == G_1, por lo que no se requiere más iteración, y podemos detenernos aquí.
Implementación de K-Means usando Python:
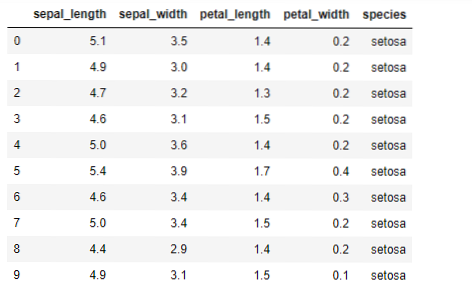
Ahora, vamos a implementar el algoritmo K-means en Python. Para implementar las K-medias, usaremos el famoso conjunto de datos Iris, que es de código abierto. Este conjunto de datos tiene tres clases diferentes. Este conjunto de datos tiene básicamente cuatro características: Longitud del sépalo, ancho del sépalo, largo del pétalo y ancho del pétalo. La última columna dirá el nombre de la clase de esa fila como setosa.
El conjunto de datos tiene el siguiente aspecto:
Para la implementación de python k-means, necesitamos importar las bibliotecas requeridas. Así que importamos Pandas, Numpy, Matplotlib y también KMeans de sklearn.clutser como se indica a continuación:

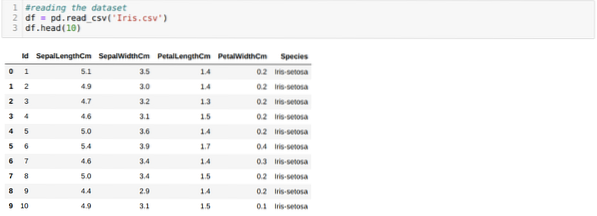
Estamos leyendo el iris.csv dataset usando el método read_csv panda y mostrará los 10 mejores resultados usando el método head.
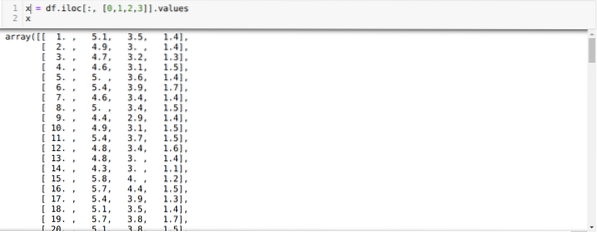
Ahora, estamos leyendo solo aquellas características del conjunto de datos que requerimos para entrenar el modelo. Entonces, estamos leyendo las cuatro características de los conjuntos de datos (longitud del sépalo, ancho del sépalo, largo del pétalo, ancho del pétalo). Para eso, pasamos los cuatro valores de índice [0, 1, 2, 3] a la función iloc del marco de datos del panda (df) como se muestra a continuación:
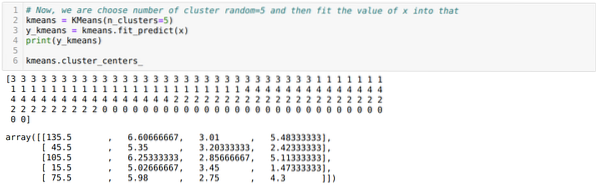
Ahora, elegimos el número de conglomerados al azar (K = 5). Creamos el objeto de la clase K-means y luego ajustamos nuestro conjunto de datos x en ese para entrenamiento y predicción como se muestra a continuación:
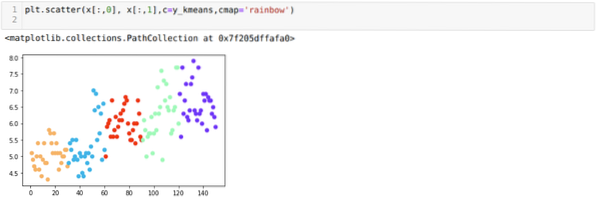
Ahora, vamos a visualizar nuestro modelo con el valor aleatorio de K = 5. Podemos ver claramente cinco grupos, pero parece que no es exacto, como se muestra a continuación.
Entonces, nuestro siguiente paso es averiguar si el número de clústeres era correcto o no. Y para eso usamos el método del codo. El método Elbow se utiliza para averiguar el número óptimo del clúster para un conjunto de datos en particular. Este método se utilizará para averiguar si el valor de k = 5 era correcto o no, ya que no estamos obteniendo una agrupación clara. Entonces, después de eso, pasamos al siguiente gráfico, que muestra que el valor de K = 5 no es correcto porque el valor óptimo está entre 3 o 4.
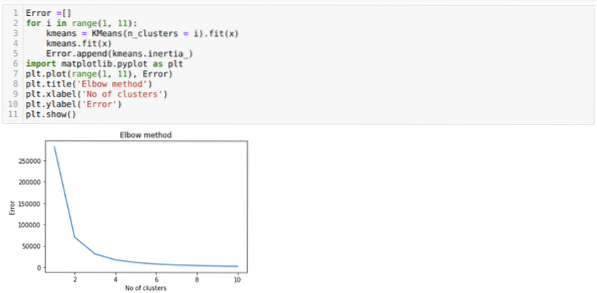
Ahora, vamos a ejecutar el código anterior nuevamente con el número de clústeres K = 4 como se muestra a continuación:
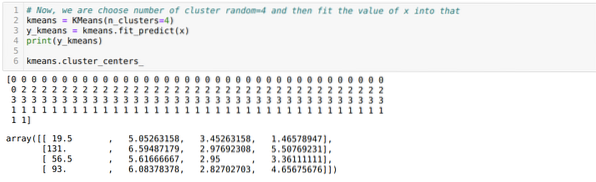
Ahora, vamos a visualizar la agrupación de nuevas compilaciones K = 4 anterior. La siguiente pantalla muestra que ahora la agrupación se realiza a través de k-means.
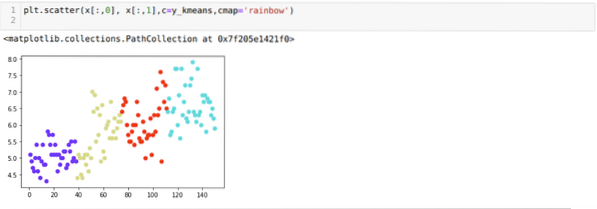
Conclusión
Entonces, estudiamos el algoritmo K-means tanto en código numérico como en código Python. También hemos visto cómo podemos averiguar la cantidad de clústeres para un conjunto de datos en particular. A veces, el método Elbow no puede dar el número correcto de grupos, por lo que en ese caso, hay varios métodos que podemos elegir.
 Phenquestions
Phenquestions