Como SciPy es de código abierto, Tiene una comunidad de desarrolladores muy activa y vibrante debido a la cual hay una enorme cantidad de módulos presentes para una gran cantidad de aplicaciones científicas y cálculos disponibles con SciPy. Algunas de las complejas operaciones matemáticas que se pueden realizar con SciPy son:
- Interpolación
- Integración
- Mejoramiento
- Procesamiento de imágenes
- Estadísticas
- Cálculos de funciones especiales, etc.
SciPy se puede comparar con la mayoría de las bibliotecas estándar y de comandos, como la biblioteca GSL para C ++ y Matlab. Como SciPy está construido sobre el paquete NumPy, estos dos paquetes también se pueden integrar completamente. Si puede pensar en una operación matemática que deba realizarse, asegúrese de verificar la biblioteca SciPy antes de implementar ese módulo por su cuenta, porque en la mayoría de los casos, SciPy ya tiene todas las operaciones completamente implementadas.
Instalar la biblioteca SciPy
Instalemos la biblioteca SciPy antes de pasar a los ejemplos y conceptos reales. Hay dos formas de instalar este paquete. El primero incluye el uso del administrador de paquetes de Python, pip:
pip instalar scipyLa segunda forma se relaciona con Anaconda, podemos instalar el paquete como:
conda install -c anaconda scipyUna vez instalada la biblioteca, podemos importarla como:
importar scipyFinalmente, como también usaremos NumPy (se recomienda que para todas las operaciones de NumPy, usemos NumPy directamente en lugar de pasar por el paquete SciPy):
importar numpyEs posible que en algunos casos, también nos guste trazar nuestros resultados para lo cual usaremos la biblioteca Matplotlib. Realice la siguiente importación para esa biblioteca:
importar matplotlibUsaré el administrador de Anaconda para todos los ejemplos de esta lección. Lanzaré un Jupyter Notebook para lo mismo:

Ahora que estamos listos con todas las declaraciones de importación para escribir algo de código, comencemos a sumergirnos en el paquete SciPy con algunos ejemplos prácticos.
Trabajar con ecuaciones polinomiales
Comenzaremos mirando ecuaciones polinomiales simples. Hay dos formas en las que podemos integrar funciones polinomiales en nuestro programa. Podemos hacer uso de poly1d clase que hace uso de coeficientes o las raíces de un polinomio para inicializar un polinomio. Veamos un ejemplo:
desde numpy import poly1dprimer_polinomio = poli1d ([3, 4, 7])
imprimir (primer polinomio)
Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

Claramente, la representación polinomial de la ecuación se imprime como salida, por lo que el resultado es bastante fácil de entender. También podemos realizar varias operaciones en este polinomio, como elevarlo al cuadrado, encontrar su derivada o incluso resolverlo para un valor de x. Intentemos hacer todo esto en el siguiente ejemplo:
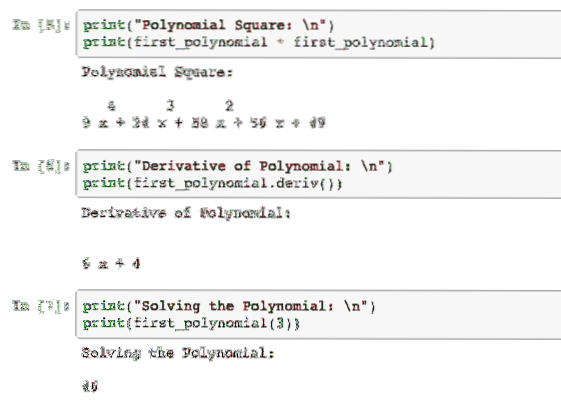
print ("Polinomio Cuadrado: \ n")imprimir (primer polinomio * primer polinomio)
print ("Derivada de polinomio: \ n")
imprimir (primer polinomio.deriv ())
print ("Resolviendo el polinomio: \ n")
imprimir (primer polinomio (3))
Cuando ejecutemos este ejemplo, veremos el siguiente resultado:
Justo cuando pensaba que esto es todo lo que podíamos hacer con SciPy, recordé que también podemos integrar un polinomio. Ejecutemos un ejemplo final con polinomios:
print ("Integrando el polinomio: \ n")imprimir (primer polinomio.integ (1))
El entero que pasamos le dice al paquete cuántas veces integrar el polinomio:
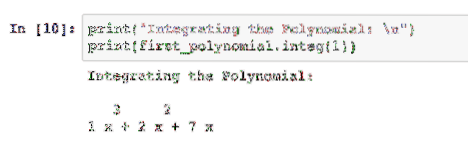
Simplemente podemos pasar otro entero que le dice al paquete cuántas veces debe integrar este polinomio.
Resolver ecuaciones lineales
Incluso es posible resolver ecuaciones lineales con SciPy y encontrar sus raíces, si existen. Para resolver ecuaciones lineales, representamos el conjunto de ecuaciones como matrices NumPy y su solución como matrices NumPy separadas. Visualicémoslo con un ejemplo donde hacemos lo mismo y usamos linalg paquete para encontrar las raíces de las ecuaciones, aquí están las ecuaciones que resolveremos:
1x + 5y = 63x + 7y = 9
Resolvamos las ecuaciones anteriores:
de scipy import linalgecuación = np.matriz ([[1, 5], [3, 7]])
solución = np.matriz ([[6], [9]])
raíces = linalg.resolver (ecuación, solución)
print ("Encontré las raíces:")
imprimir (raíces)
print ("\ n El producto escalar debe ser cero si las soluciones son correctas:")
imprimir (ecuación.dot (raíces) - solución)
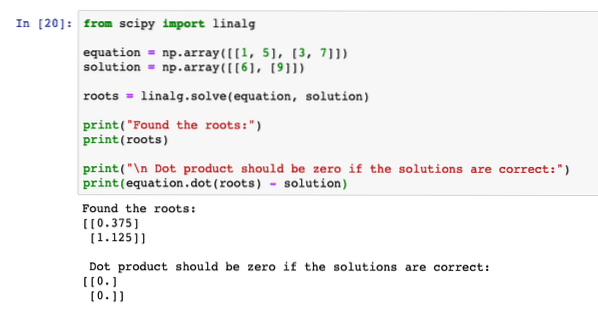
Cuando ejecutamos el programa anterior, veremos que la ecuación del producto escalar da un resultado cero, lo que significa que las raíces que encontró el programa eran correctas:
Transformaciones de Fourier con SciPy
Las transformaciones de Fourier nos ayudan a expresar una función como componentes separados que componen esa función y nos guía sobre la forma en que podemos recombinar esos componentes para recuperar la función original.
Veamos un ejemplo simple de transformaciones de Fourier donde graficamos la suma de dos cosenos usando la biblioteca Matplotlib:
de scipy.fftpack importar fft# Número de puntos de muestra
N = 500
# espaciado de muestra
T = 1.0/800.0
x = np.linspace (0.0, N * T, N)
y = np.porque (50.0 * 2.0 * np.pi * x) + 0.5 * np.porque (80.0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.linspace (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib para fines de trazado
importar matplotlib.pyplot como plt
plt.parcela (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.título ('Información')
plt.ylabel ('eje Y')
plt.xlabel ('eje X')
plt.red()
plt.show()
Aquí, comenzamos construyendo un espacio muestral y una ecuación de coseno que luego transformamos y graficamos. Aquí está el resultado del programa anterior:
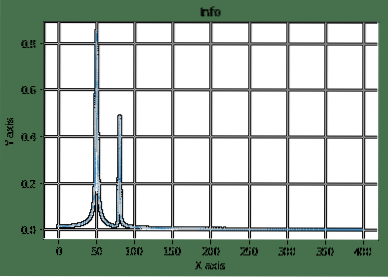
Este es uno de los buenos ejemplos en los que vemos que SciPy se usa en una ecuación matemática compleja para visualizar las cosas fácilmente.
Vectores y Matrix con SciPy
Ahora que sabemos muchas cosas de las que SciPy es capaz, podemos estar seguros de que SciPy también puede funcionar con Vectores y Matrix. Las matrices son una parte importante del álgebra lineal, ya que las matrices también son algo que usamos para representar mapeos vectoriales.
Al igual que vimos resolver ecuaciones lineales con SciPy, podemos representar vectores con notario público.formación() funciones. Comencemos construyendo una matriz:
my_matrix = np.matriz (np.aleatorio.aleatorio ((3, 3)))imprimir (my_matrix)
Aquí está el resultado del fragmento anterior:

Siempre que hablamos de matrices, siempre hablamos de autovalores y autovectores. En pocas palabras, los vectores propios son los vectores que, cuando se multiplican con una matriz, no cambian de dirección, a diferencia de la mayoría de los vectores. Esto significa que incluso cuando multiplica un vector propio con una matriz, existe un valor (o valor propio) que es uno de los factores de la multiplicación. Esto significa:
Ax = λx.En la ecuación anterior, A es la matriz, λ es el valor propio y x es el vector. Escribamos un fragmento de código simple para encontrar los valores propios de un vector dado:
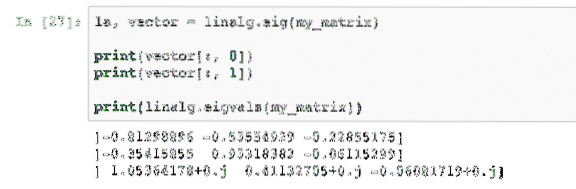
la, vector = linalg.eig (my_matrix)imprimir (vector [:, 0])
imprimir (vector [:, 1])
imprimir (linalg.eigvals (my_matrix))
Cuando ejecutemos este ejemplo, veremos el siguiente resultado:
Calcular el determinante de la matriz
La siguiente operación que realizaremos con SciPy es calcular el determinante de una matriz bidimensional. Reutilizaremos la matriz que usamos en el último fragmento de código aquí:
linalg.det (mi_matriz)Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

Conclusión
En esta lección, analizamos muchos buenos ejemplos en los que SciPy puede ayudarnos al realizar cálculos matemáticos complejos para nosotros con una API y paquetes fáciles de usar.
 Phenquestions
Phenquestions