Tutorial de Python Tensorflow

En esta lección, veremos TensorFlow, que es una biblioteca de aprendizaje automático de código abierto que se utiliza para diseñar, construir y entrenar modelos de aprendizaje profundo. Es posible realizar cálculos numéricos con la biblioteca TensorFlow, cuyos gráficos de flujo de datos en los que las operaciones matemáticas se representan como nodos y los datos se representan como bordes entre esos nodos.

En general, cubriremos tres temas principales en esta lección:

1. ¿Qué son los tensores y TensorFlow?
2. Aplicar algoritmos de AA con TensorFlow
3. Casos de uso de TensorFlow

TensorFlow es un excelente paquete de Python de Google que hace un buen uso del paradigma de programación de flujo de datos para cálculos matemáticos altamente optimizados. Algunas de las características de TensorFlow son:

• Capacidad de cálculo distribuido que facilita la gestión de datos en grandes conjuntos
• El aprendizaje profundo y el soporte de redes neuronales son buenos
• Gestiona estructuras matemáticas complejas como matrices n-dimensionales de manera muy eficiente

Debido a todas estas características y a la variedad de algoritmos de aprendizaje automático que implementa TensorFlow, es una biblioteca a escala de producción. Profundicemos en los conceptos de TensorFlow para que podamos ensuciarnos las manos con el código justo después.

Instalación de TensorFlow

Como usaremos la API de Python para TensorFlow, es bueno saber que funciona tanto con Python 2.7 y 3.3+ versiones. Instalemos la biblioteca de TensorFlow antes de pasar a los ejemplos y conceptos reales. Hay dos formas de instalar este paquete. El primero incluye el uso del administrador de paquetes de Python, pip:

pip instalar tensorflow

La segunda forma se relaciona con Anaconda, podemos instalar el paquete como:

conda install -c conda-forge tensorflow

No dude en buscar versiones de GPU y compilaciones nocturnas en las páginas de instalación oficiales de TensorFlow.

Usaré el administrador de Anaconda para todos los ejemplos de esta lección. Lanzaré un Jupyter Notebook para lo mismo:

Ahora que estamos listos con todas las declaraciones de importación para escribir algo de código, comencemos a sumergirnos en el paquete SciPy con algunos ejemplos prácticos.

¿Qué son los tensores??

Los tensores son las estructuras de datos básicas que se utilizan en Tensorflow. Sí, son solo una forma de representar datos en el aprendizaje profundo. Visualicémoslos aquí:

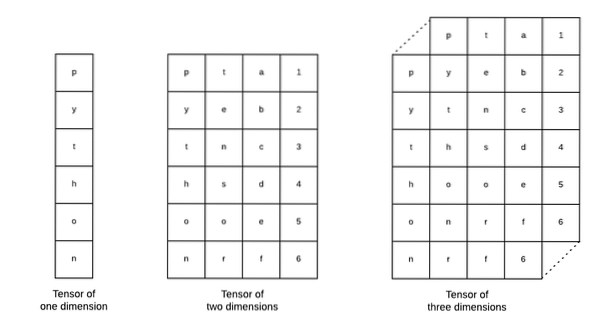
Como se describe en la imagen, Los tensores se pueden denominar matriz n-dimensional que nos permite representar datos en dimensiones complejas. Podemos pensar en cada dimensión como una característica diferente de los datos en el aprendizaje profundo. Esto significa que los tensores pueden llegar a ser bastante complejos cuando se trata de conjuntos de datos complejos con muchas características.

Una vez que sepamos qué son los tensores, creo que es bastante fácil derivar lo que sucede en TensorFlow. Ese término significa cómo los tensores o características pueden fluir en conjuntos de datos para producir resultados valiosos a medida que realizamos varias operaciones en ellos.

Comprender TensorFlow con constantes

Tal como leímos anteriormente, TensorFlow nos permite realizar algoritmos de aprendizaje automático en tensores para producir resultados valiosos. Con TensorFlow, diseñar y entrenar modelos de Deep Learning es sencillo.

TensorFlow viene con la construcción Gráficos de cálculo. Los gráficos de cálculo son los gráficos de flujo de datos en los que las operaciones matemáticas se representan como nodos y los datos se representan como bordes entre esos nodos. Escribamos un fragmento de código muy simple para proporcionar una visualización concreta:

importar tensorflow como tf
x = tf.constante (5)
y = tf.constante (6)
z = x * y
imprimir (z)

Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

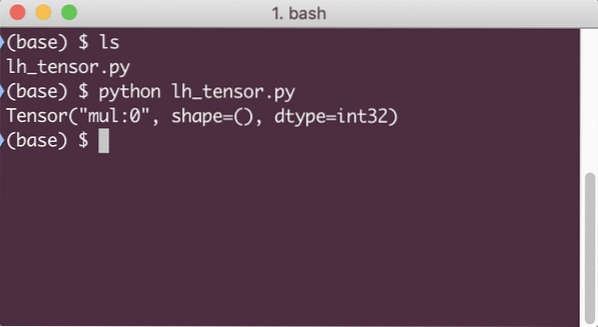
¿Por qué la multiplicación es incorrecta?? Eso no era lo que esperábamos. Esto sucedió porque no es así como podemos realizar operaciones con TensorFlow. Primero, necesitamos comenzar un sesión para que el gráfico de cálculo funcione,

Con Sessions, podemos encapsular el control de operaciones y estado de tensores. Esto significa que una sesión también puede almacenar el resultado de un gráfico de cálculo para que pueda pasar ese resultado a la siguiente operación en el orden de ejecución de las canalizaciones. Creemos una sesión ahora para obtener el resultado correcto:

# Comience con el objeto de sesión
sesión = tf.Sesión()
# Proporcionar el cálculo a la sesión y almacenarlo
resultado = sesión.correr (z)
# Imprime el resultado del cálculo
imprimir (resultado)
# Cerrar la sesión
sesión.cerca()

Esta vez, obtuvimos la sesión y le proporcionamos el cálculo que necesita para ejecutarse en los nodos. Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

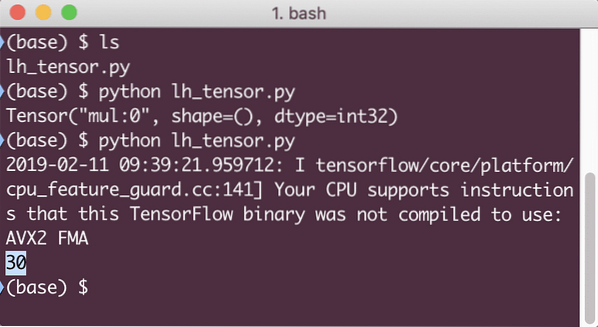
Aunque recibimos una advertencia de TensorFlow, aún obtuvimos el resultado correcto del cálculo.

Operaciones de tensor de un solo elemento

Al igual que multiplicamos dos tensores constantes en el último ejemplo, tenemos muchas otras operaciones en TensorFlow que se pueden realizar en elementos individuales:

• agregar
• sustraer
• multiplicar
• div
• modificación
• abdominales
• negativo
• firmar
• cuadrado
• redondo
• sqrt
• pow
• Exp
• Iniciar sesión
• máximo
• mínimo
• porque
• pecado

Las operaciones de un solo elemento significan que incluso cuando proporciona una matriz, las operaciones se realizarán en cada uno de los elementos de esa matriz. Por ejemplo:

importar tensorflow como tf
importar numpy como np
tensor = np.matriz ([2, 5, 8])
tensor = tf.convert_to_tensor (tensor, dtype = tf.float64)
con tf.Session () como sesión:
imprimir (sesión.correr (tf.cos (tensor)))

Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

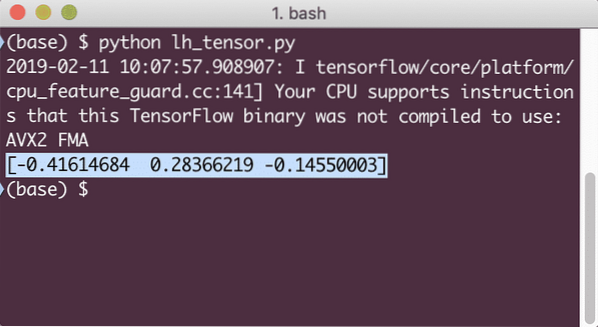
Entendimos dos conceptos importantes aquí:

1. Cualquier matriz NumPy se puede convertir fácilmente en un tensor con la ayuda de la función convert_to_tensor
2. La operación se realizó en cada uno de los elementos de la matriz NumPy

Marcadores de posición y variables

En una de las secciones anteriores, vimos cómo podemos usar las constantes de Tensorflow para hacer gráficos computacionales. Pero TensorFlow también nos permite tomar entradas sobre la marcha para que el gráfico de cálculo pueda ser de naturaleza dinámica. Esto es posible con la ayuda de marcadores de posición y variables.

En realidad, los marcadores de posición no contienen ningún dato y se deben proporcionar entradas válidas durante el tiempo de ejecución y, como se esperaba, sin una entrada, generarán un error.

Un marcador de posición se puede denominar como un acuerdo en un gráfico de que seguramente se proporcionará una entrada en tiempo de ejecución. A continuación, se muestra un ejemplo de marcadores de posición:

importar tensorflow como tf
# Dos marcadores de posición
x = tf. marcador de posición (tf.float32)
y = tf. marcador de posición (tf.float32)
# Asignación de la operación de multiplicación w.r.t. a & b al nodo mul
z = x * y
# Crea una sesión
sesión = tf.Sesión()
# Pasar valores para placehollders
resultado = sesión.ejecutar (z, x: [2, 5], y: [3, 7])
print ('Multiplicar xey:', resultado)

Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

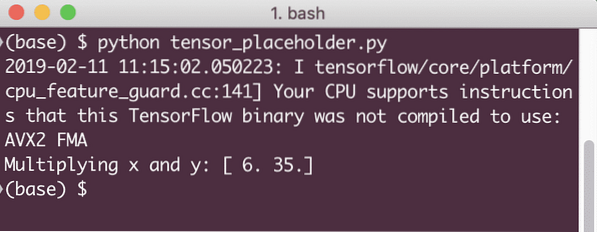
Ahora que tenemos conocimiento sobre los marcadores de posición, volvamos nuestra mirada hacia las variables. Sabemos que la salida de una ecuación puede cambiar para el mismo conjunto de entradas a lo largo del tiempo. Entonces, cuando entrenamos nuestra variable modelo, puede cambiar su comportamiento con el tiempo. En este escenario, una variable nos permite agregar estos parámetros entrenables a nuestro gráfico computacional. Una variable se puede definir de la siguiente manera:

x = tf.Variable ([5.2], dtype = tf.float32)

En la ecuación anterior, x es una variable a la que se le proporciona su valor inicial y el tipo de datos. Si no proporcionamos el tipo de datos, TensorFlow lo inferirá con su valor inicial. Consulte los tipos de datos de TensorFlow aquí.

A diferencia de una constante, necesitamos llamar a una función de Python para inicializar todas las variables de un gráfico:

init = tf.global_variables_initializer ()
sesión.ejecutar (init)

Asegúrese de ejecutar la función TensorFlow anterior antes de hacer uso de nuestro gráfico.

Regresión lineal con TensorFlow

La regresión lineal es uno de los algoritmos más comunes que se utilizan para establecer una relación en un dato continuo dado. Esta relación entre los puntos de coordenadas, digamos xey, se llama hipótesis. Cuando hablamos de regresión lineal, la hipótesis es una línea recta:

y = mx + c

Aquí, m es la pendiente de la línea y aquí, es un vector que representa pesos. c es el coeficiente constante (intersección con el eje y) y aquí, representa el Parcialidad. El peso y el sesgo se denominan parámetros del modelo.

Las regresiones lineales nos permiten estimar los valores de ponderación y sesgo de manera que tengamos un mínimo función de costo. Finalmente, x es la variable independiente en la ecuación e y es la variable dependiente. Ahora, comencemos a construir el modelo lineal en TensorFlow con un fragmento de código simple que explicaremos:

importar tensorflow como tf
# Variables para la pendiente del parámetro (W) con valor inicial como 1.1
W = tf.Variable ([1.1], tf.float32)
# Variable de sesgo (b) con valor inicial como -1.1
b = tf.Variable ([- 1.1], tf.float32)
# Marcadores de posición para proporcionar entrada o variable independiente, denotados por x
x = tf.marcador de posición (tf.float32)
# Ecuación de línea o regresión lineal
modelo_lineal = W * x + b
# Inicializando todas las variables
sesión = tf.Sesión()
init = tf.global_variables_initializer ()
sesión.ejecutar (init)
# Ejecutar modelo de regresión
imprimir (sesión.ejecutar (modelo_lineal x: [2, 5, 7, 9]))

Aquí, hicimos exactamente lo que explicamos anteriormente, resumamos aquí:

• Comenzamos importando TensorFlow en nuestro script
• Cree algunas variables para representar el peso del vector y el sesgo del parámetro
• Se necesitará un marcador de posición para representar la entrada, x
• Representar el modelo lineal
• Inicializar todos los valores necesarios para el modelo

Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

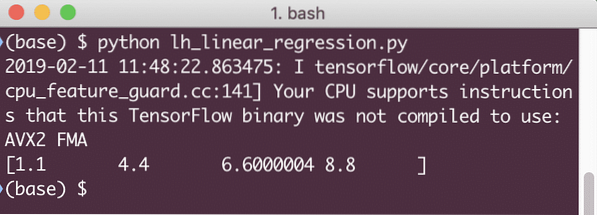
El fragmento de código simple solo proporciona una idea básica sobre cómo podemos construir un modelo de regresión. Pero aún necesitamos hacer algunos pasos más para completar el modelo que construimos:

• Necesitamos hacer que nuestro modelo se entrene a sí mismo para que pueda producir resultados para cualquier entrada dada
• Necesitamos validar la salida proporcionada por el modelo comparándola con la salida esperada para un x dado

Función de pérdida y validación del modelo

Para validar el modelo, necesitamos tener una medida de qué tan desviada está la salida de corriente de la salida esperada. Hay varias funciones de pérdida que se pueden utilizar aquí para la validación, pero veremos uno de los métodos más comunes, Suma del error al cuadrado o SSE.

La ecuación para SSE se da como:

E = 1/2 * (t - y) 2

Aquí:

• E = Error cuadrático medio
• t = Salida recibida
• y = Salida esperada
• t - y = Error

Ahora, escribamos un fragmento de código a continuación del último fragmento para reflejar el valor de pérdida:

y = tf.marcador de posición (tf.float32)
error = modelo_lineal - y
cuadrados_errores = tf.cuadrado (error)
pérdida = tf.suma_reducida (errores_cuadrados)
imprimir (sesión.correr (pérdida, x: [2, 5, 7, 9], y: [2, 4, 6, 8]))

Cuando ejecutemos este ejemplo, veremos el siguiente resultado:

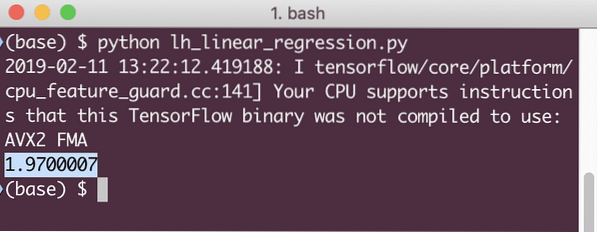
Claramente, el valor de pérdida es muy bajo para el modelo de regresión lineal dado.

Conclusión

En esta lección, analizamos uno de los paquetes de aprendizaje profundo y aprendizaje automático más populares, TensorFlow. También hicimos un modelo de regresión lineal que tenía una precisión muy alta.