La biblioteca NumPy nos permite realizar varias operaciones que deben realizarse en estructuras de datos que se utilizan a menudo en el aprendizaje automático y la ciencia de datos, como vectores, matrices y matrices. Solo mostraremos las operaciones más comunes con NumPy que se utilizan en muchas canalizaciones de Machine Learning. Finalmente, tenga en cuenta que NumPy es solo una forma de realizar las operaciones, por lo tanto, las operaciones matemáticas que mostramos son el enfoque principal de esta lección y no el paquete NumPy en sí. Empecemos.
¿Qué es un vector??
Según Google, un vector es una cantidad que tiene dirección y magnitud, especialmente para determinar la posición de un punto en el espacio con respecto a otro.
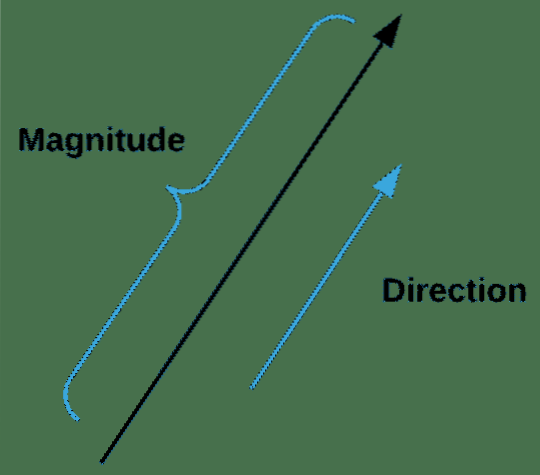
Los vectores son muy importantes en el aprendizaje automático, ya que no solo describen la magnitud sino también la dirección de las características. Podemos crear un vector en NumPy con el siguiente fragmento de código:
importar numpy como npvector_fila = np.matriz ([1,2,3])
imprimir (vector_fila)
En el fragmento de código anterior, creamos un vector de fila. También podemos crear un vector de columna como:
importar numpy como npcol_vector = np.matriz ([[1], [2], [3]])
imprimir (col_vector)
Haciendo una matriz
Una matriz puede entenderse simplemente como una matriz bidimensional. Podemos hacer una matriz con NumPy haciendo una matriz multidimensional:
matriz = np.matriz ([[1, 2, 3], [4, 5, 6], [7, 8, 9]])imprimir (matriz)
Aunque la matriz es exactamente similar a la matriz multidimensional, no se recomienda la estructura de datos matriciales por dos razones:
- La matriz es el estándar cuando se trata del paquete NumPy
- La mayoría de las operaciones con NumPy devuelven matrices y no una matriz
Usando una matriz dispersa
Para recordar, una matriz dispersa es aquella en la que la mayoría de los elementos son cero. Ahora, un escenario común en el procesamiento de datos y el aprendizaje automático es el procesamiento de matrices en las que la mayoría de los elementos son cero. Por ejemplo, considere una matriz cuyas filas describen todos los videos en Youtube y las columnas representan a cada usuario registrado. Cada valor representa si el usuario ha visto un video o no. Por supuesto, la mayoría de los valores de esta matriz serán cero. La ventaja con matriz dispersa es que no almacena los valores que son cero. Esto da como resultado una gran ventaja computacional y también una optimización del almacenamiento.
Creemos una matriz de chispas aquí:
de scipy import sparsematriz_original = np.matriz ([[1, 0, 3], [0, 0, 6], [7, 0, 0]])
sparse_matrix = disperso.csr_matrix (original_matrix)
imprimir (matriz_espasa)
Para comprender cómo funciona el código, veremos el resultado aquí:
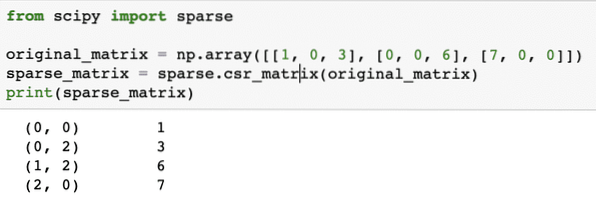
En el código anterior, usamos la función de NumPy para crear un Fila dispersa comprimida matriz donde los elementos distintos de cero se representan utilizando los índices de base cero. Hay varios tipos de matrices dispersas, como:
- Columna dispersa comprimida
- Lista de listas
- Diccionario de claves
No nos sumergiremos en otras matrices escasas aquí, pero sepa que cada uno de sus usos es específico y nadie puede ser calificado como el "mejor".
Aplicar operaciones a todos los elementos vectoriales
Es un escenario común cuando necesitamos aplicar una operación común a múltiples elementos vectoriales. Esto se puede hacer definiendo una lambda y luego vectorizando la misma. Veamos un fragmento de código para el mismo:
matriz = np.formación([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
mul_5 = lambda x: x * 5
vectorized_mul_5 = np.vectorizar (mul_5)
vectorized_mul_5 (matriz)
Para comprender cómo funciona el código, veremos el resultado aquí:

En el fragmento de código anterior, usamos la función vectorizar que es parte de la biblioteca NumPy, para transformar una definición lambda simple en una función que puede procesar todos y cada uno de los elementos del vector. Es importante tener en cuenta que vectorizar es solo un bucle sobre los elementos y no tiene ningún efecto en el rendimiento del programa. NumPy también permite radiodifusión, lo que significa que en lugar del código complejo anterior, podríamos haber hecho simplemente:
matriz * 5Y el resultado hubiera sido exactamente el mismo. Primero quería mostrar la parte compleja; de lo contrario, se habría saltado la sección!
Media, varianza y desviación estándar
Con NumPy, es fácil realizar operaciones relacionadas con estadísticas descriptivas sobre vectores. La media de un vector se puede calcular como:
notario público.media (matriz)La varianza de un vector se puede calcular como:
notario público.var (matriz)La desviación estándar de un vector se puede calcular como:
notario público.std (matriz)La salida de los comandos anteriores en la matriz dada se da aquí:

Transposición de una matriz
La transposición es una operación muy común de la que oirá hablar cada vez que esté rodeado de matrices. La transposición es solo una forma de intercambiar valores de columnas y filas de una matriz. Tenga en cuenta que un el vector no se puede transponer como un vector es solo una colección de valores sin que esos valores se categoricen en filas y columnas. Tenga en cuenta que convertir un vector de fila en un vector de columna no es una transposición (según las definiciones del álgebra lineal, que está fuera del alcance de esta lección).
Por ahora, encontraremos la paz con solo trasponer una matriz. Es muy sencillo acceder a la transposición de una matriz con NumPy:
matriz.TLa salida del comando anterior en la matriz dada se da aquí:
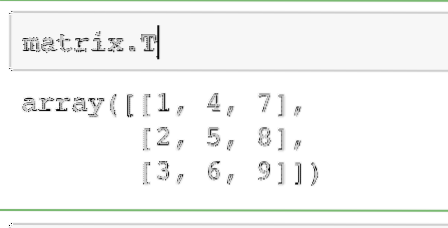
Se puede realizar la misma operación en un vector de fila para convertirlo en un vector de columna.
Aplanar una matriz
Podemos convertir una matriz en una matriz unidimensional si deseamos procesar sus elementos de forma lineal. Esto se puede hacer con el siguiente fragmento de código:
matriz.aplanar()La salida del comando anterior en la matriz dada se da aquí:

Tenga en cuenta que la matriz plana es una matriz unidimensional, simplemente lineal en la moda.
Cálculo de autovalores y autovectores
Los vectores propios se utilizan con mucha frecuencia en los paquetes de aprendizaje automático. Entonces, cuando una función de transformación lineal se presenta como una matriz, entonces X, los vectores propios son los vectores que cambian solo en la escala del vector, pero no en su dirección. Podemos decir eso:
Xv = γvAquí, X es la matriz cuadrada y γ contiene los valores propios. Además, v contiene los vectores propios. Con NumPy, es fácil calcular valores propios y vectores propios. Aquí está el fragmento de código donde demostramos lo mismo:
evalues, evectors = np.linalg.eig (matriz)La salida del comando anterior en la matriz dada se da aquí:
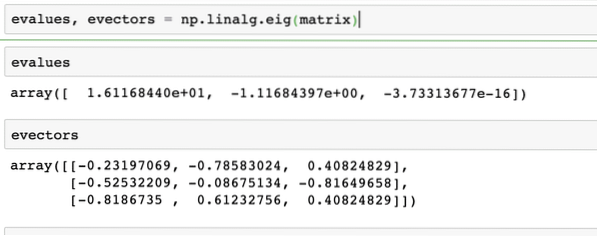
Productos punto de vectores
Productos punto de vectores es una forma de multiplicar 2 vectores. Te habla de cuántos de los vectores están en la misma dirección, a diferencia del producto cruzado que le dice lo contrario, qué tan pequeños son los vectores en la misma dirección (llamado ortogonal). Podemos calcular el producto escalar de dos vectores como se indica en el fragmento de código aquí:
a = np.matriz ([3, 5, 6])b = np.matriz ([23, 15, 1])
notario público.punto (a, b)
La salida del comando anterior en las matrices dadas se da aquí:

Sumar, restar y multiplicar matrices
Sumar y restar múltiples matrices es una operación bastante sencilla en matrices. Hay dos formas de hacer esto. Veamos el fragmento de código para realizar estas operaciones. Con el fin de mantener esto simple, usaremos la misma matriz dos veces:
notario público.agregar (matriz, matriz)A continuación, se pueden restar dos matrices como:
notario público.restar (matriz, matriz)La salida del comando anterior en la matriz dada se da aquí:
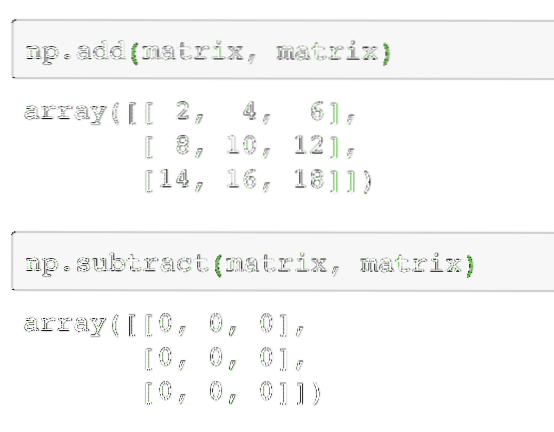
Como era de esperar, cada uno de los elementos de la matriz se suma / resta con el elemento correspondiente. Multiplicar una matriz es similar a encontrar el producto escalar como hicimos anteriormente:
notario público.punto (matriz, matriz)El código anterior encontrará el verdadero valor de multiplicación de dos matrices, dado como:
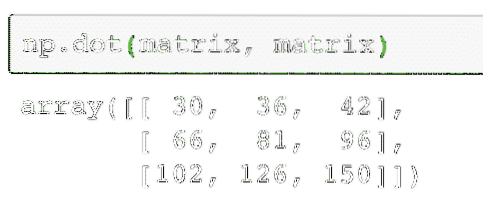
La salida del comando anterior en la matriz dada se da aquí:

Conclusión
En esta lección, analizamos muchas operaciones matemáticas relacionadas con vectores, matrices y matrices que se utilizan comúnmente en el procesamiento de datos, la estadística descriptiva y la ciencia de datos. Esta fue una lección rápida que cubrió solo las secciones más comunes e importantes de la amplia variedad de conceptos, pero estas operaciones deberían dar una muy buena idea de lo que se pueden realizar todas las operaciones al tratar con estas estructuras de datos.
Comparta sus comentarios libremente sobre la lección en Twitter con @linuxhint y @sbmaggarwal (ese soy yo!).
 Phenquestions
Phenquestions