- 1 para verdadero o
- 0 para falso
La importancia clave de la regresión logística:
- Las variables independientes no deben ser multicolinealidad; si hay alguna relación, entonces debería ser muy poco.
- El conjunto de datos para la regresión logística debe ser lo suficientemente grande para obtener mejores resultados.
- Solo esos atributos deben estar en el conjunto de datos, lo que tiene algún significado.
- Las variables independientes deben estar de acuerdo con probabilidades de registro.
Para construir el modelo del Regresión logística, usamos el scikit-learn Biblioteca. El proceso de regresión logística en Python se da a continuación:
- Importe todos los paquetes necesarios para la regresión logística y otras bibliotecas.
- Sube el conjunto de datos.
- Comprender las variables independientes del conjunto de datos y las variables dependientes.
- Divida el conjunto de datos en datos de prueba y entrenamiento.
- Inicializar el modelo de regresión logística.
- Ajustar el modelo con el conjunto de datos de entrenamiento.
- Predecir el modelo utilizando los datos de prueba y calcular la precisión del modelo.
Problema: Los primeros pasos son recopilar el conjunto de datos en el que queremos aplicar la Regresión logística. El conjunto de datos que vamos a utilizar aquí es para el conjunto de datos de admisión de MS. Este conjunto de datos tiene cuatro variables y de las cuales tres son variables independientes (GRE, GPA, work_experience) y una es una variable dependiente (admitida). Este conjunto de datos dirá si el candidato será admitido o no en una universidad prestigiosa en función de su GPA, GRE o work_experience.
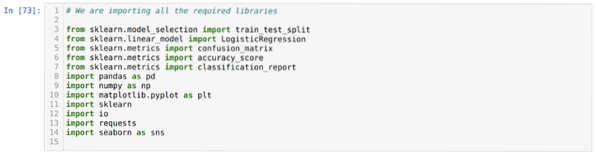
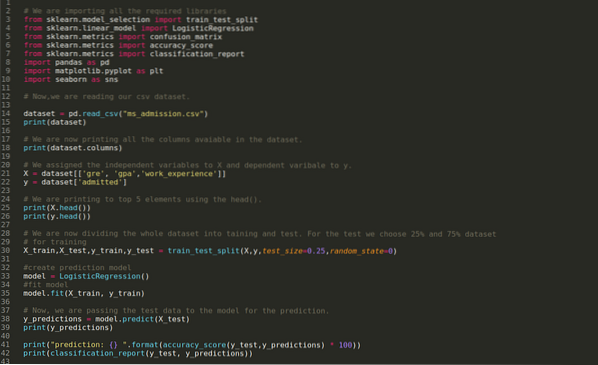
Paso 1: Importamos todas las bibliotecas requeridas que requerimos para el programa Python.
Paso 2: Ahora, estamos cargando nuestro conjunto de datos de admisión de ms usando la función read_csv pandas.

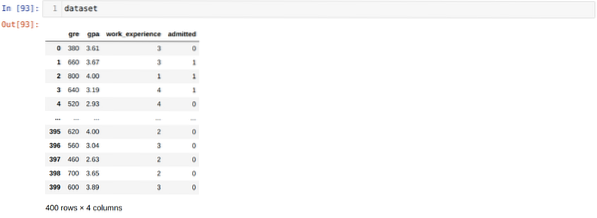
Paso 3: El conjunto de datos se ve a continuación:
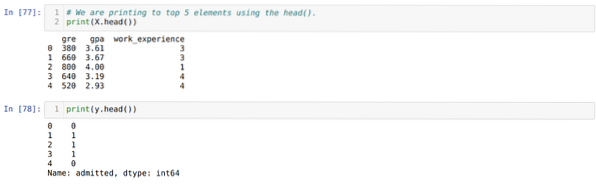
Paso 4: Verificamos todas las columnas disponibles en el conjunto de datos y luego establecemos todas las variables independientes en la variable X y las variables dependientes en y, como se muestra en la siguiente captura de pantalla.

Paso 5: Después de establecer las variables independientes en X y la variable dependiente en y, ahora estamos imprimiendo aquí para verificar X e y usando la función head pandas.
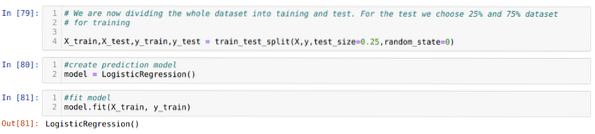
Paso 6: Ahora, vamos a dividir todo el conjunto de datos en entrenamiento y prueba. Para esto, estamos usando el método train_test_split de sklearn. Hemos entregado el 25% de todo el conjunto de datos a la prueba y el 75% restante del conjunto de datos al entrenamiento.
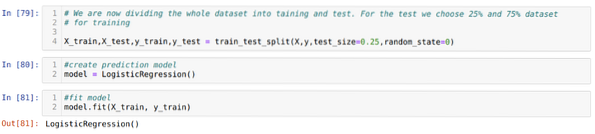
Paso 7: Ahora, vamos a dividir todo el conjunto de datos en entrenamiento y prueba. Para esto, estamos usando el método train_test_split de sklearn. Hemos entregado el 25% de todo el conjunto de datos a la prueba y el 75% restante del conjunto de datos al entrenamiento.
Luego creamos el modelo de Regresión logística y ajustamos los datos de entrenamiento.
Paso 8: Ahora, nuestro modelo está listo para la predicción, por lo que ahora estamos pasando los datos de prueba (X_test) al modelo y obtuvimos los resultados. Los resultados muestran (y_predictions) que los valores 1 (admitidos) y 0 (no admitidos).

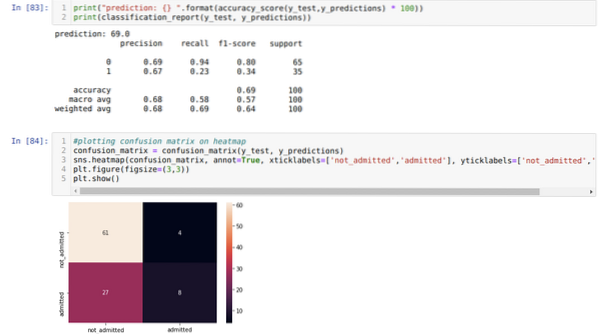
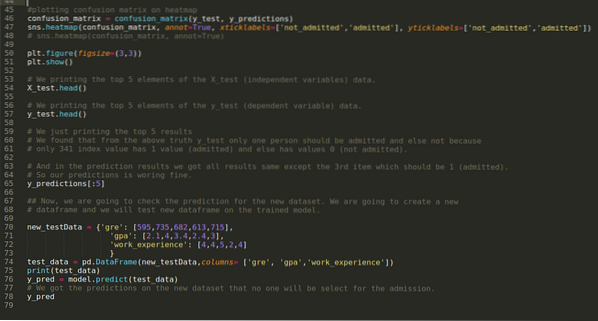
Paso 9: Ahora imprimimos el informe de clasificación y la matriz de confusión.
El informe de clasificación muestra que el modelo puede predecir los resultados con una precisión del 69%.
La matriz de confusión muestra los detalles de los datos totales de X_test como:
TP = verdaderos positivos = 8
TN = Negativos verdaderos = 61
FP = falsos positivos = 4
FN = falsos negativos = 27
Entonces, la precisión total de acuerdo con confusion_matrix es:
Precisión = (TP + TN) / Total = (8 + 61) / 100 = 0.69
Paso 10: Ahora, vamos a verificar el resultado a través de la impresión. Entonces, solo imprimimos los 5 elementos principales de X_test y y_test (valor real real) usando la función head pandas. Luego, también imprimimos los 5 primeros resultados de las predicciones como se muestra a continuación:
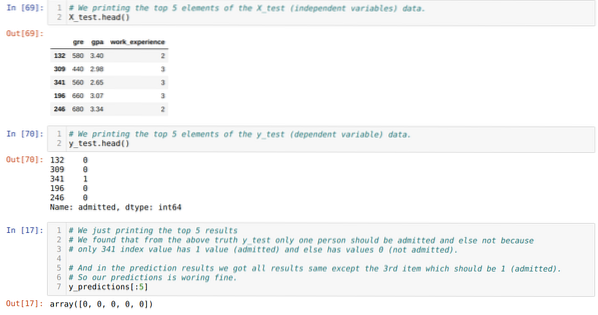
Combinamos los tres resultados en una hoja para comprender las predicciones como se muestra a continuación. Podemos ver que, a excepción de los datos de 341 X_test, que eran verdaderos (1), la predicción es falsa (0). Entonces, las predicciones de nuestro modelo funcionan en un 69%, como ya hemos mostrado anteriormente.

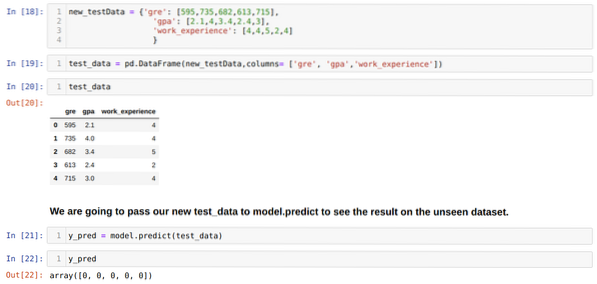
Paso 11: Entonces, entendemos cómo se realizan las predicciones del modelo en el conjunto de datos invisible como X_test. Entonces, creamos solo un nuevo conjunto de datos aleatoriamente usando un marco de datos de pandas, lo pasamos al modelo entrenado y obtuvimos el resultado que se muestra a continuación.
El código completo en Python se da a continuación:
El código de este blog, junto con el conjunto de datos, está disponible en el siguiente enlace
https: // github.com / shekharpandey89 / logistic-regression
 Phenquestions
Phenquestions


